 A
A
 B
B
 C
C A = B \ C
 A
A
 B
B
 C
C
A = B \ C
A is a 2-manifold with boundary - set difference of B and C,
B is a spherical surface,
C is a solid constructed by sweeping and set-theoretic operations.
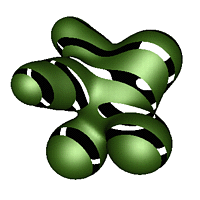 D
D
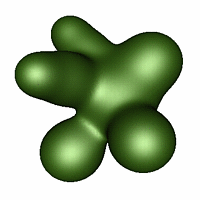 E
E
D = E \ C
D is a trimmed blobby surface - set difference of E and C,
E is a blobby surface.
This work was inspired by art works of M.C. Escher , namely "Sphere Spirals" (1958) (see them redesigned in the top figure) and "Bond of Union" (1956), showing spiral shaped surface sheets cut of a sphere and human head surfaces.
An algorithm of polygonization of trimmed implicit surfaces is presented in the paper referenced below. Such two-dimensional manifold with boundary results from the set-theoretic difference of an implicit surface and a solid. The algorithm generates the polygonal approximation of the trimmed surface with the mesh adaptation to the manifold boundary.
Pasko A.A.
"On Escher's spirals - Polygonization of 2-manifolds
with boundaries", Implicit Surfaces '98, Eurographics/ACM SIGGRAPH Workshop
(Seattle, USA, 15-16 June 1998), J. Bloomenthal and D. Saupe (Eds.),
University of Washington, ISSN 1024-0861, 1998, pp.77-80.
Electronic version: PDF (147 K)
Back to F-rep Home Page